Numerical Root Finding via Cox Rings
The Cox ring of a compact toric variety is a polynomial ring that
generalizes the homogeneous coordinate ring of projective space. It
allows to construct the toric variety as the quotient of an affine space
(minus the `base locus') by the action of a group. The construction is
introduced in a wonderful paper by David Cox.
A
0-dimensional system of Laurent polynomials, under some mild
conditions, defines a finite set of isolated points on a compact toric
variety and each point can be represented by a set of homogeneous
coordinates. In my new preprint I propose a numerical eigenvalue method to find these homogeneous coordinates.
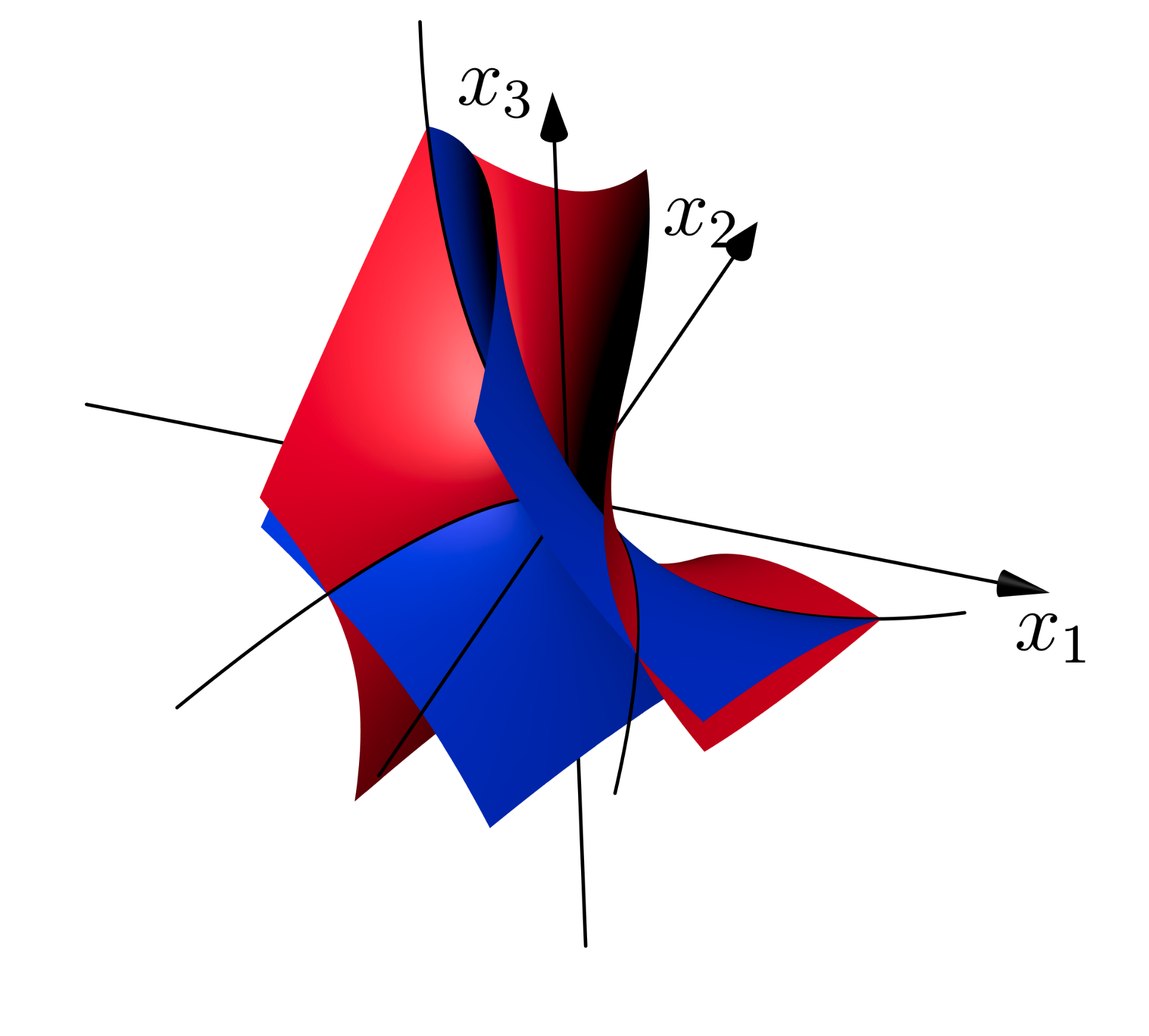
The picture above illustrates an example where the toric variety is weighted projective space with weights (1,2,1). The Cox ring in this example is the polynomial ring in three variables. We consider two Laurent polynomials whose homogenizations each define a surface in affine 3-space (which is the spectrum of the Cox ring). The real parts of these surfaces are shown in the figure. Their intersection is the union of two orbits (black curves in the figure) of the action of the reductive group, which correspond to the two solutions of the system of equations.
